Life Testing and Reliability Predictions for Electromechanical Relays
Life tests for electromechanical relays can be set up using relatively small sample sizes, typically less than 28 relays. Predictions can be made with reasonably high confidence using the two-parameter Weibull distribution, ß (Beta) and  (Eta). Increasing the operating frequency, typically running in the range of 25 to 200 Hz, can easily accelerate the life test. This acceleration allows the device to be run well into its design life, providing opportunity for failures and good statistical data.
Life Testing
Life tests for relays can be set up running 28 or fewer parts and are generally run to several hundred million operations (cycles). Since relays only age when actually switched, increasing the switching frequency can easily accelerate aging. Typically dry-reed relays are specified for several hundred million operations over a period of several years. The life period can usually be accelerated to several weeks by running the device in the range of 25 to 200 Hz. Most relays used in ATE and communications hardware have operate and release times less than one millisecond, allowing them to easily operate at these frequencies.
The life test is set up to monitor every operation on each relay, with a miss limit typically set for 1 Ohm and a stick limit set for 0.5 Volt. The load needs to be defined and should be based upon the application requirements. For example, if the relay will switch a 10 Volts/5 mA resistive load in the application, then the life test should duplicate this condition. Life tests can also be set up with capacitive and inductive loads, depending upon the application. Both capacitive and inductive loads can have high peak currents and require compensation to prevent shortened relay life.
Using Weibull to Establish Sample Size
Assuming that the underlying distribution is Weibull, this method can be used to establish the minimum sample size for a life test. The total number of units can be determined that will provide the desired confidence level in the testing. A 90% confidence bound can be calculated using the following equation:
where
t: total number of test cycles
: number of cycles where 63.2% of the population has failed (characteristic life)
n: sample size
ß: slope parameter (ß<1 indicates infancy, b=1 random failure rate, ß>1 wear out)
Table 1 is constructed based upon this equation.
Table 1
 From this chart it can be seen that for a t/ ratio between 0.01 and 0.80 the sample size can be less than 28. High confidence can be obtained for total run cycles within 1% to 80% of the characteristic life. For dry-reed relays the characteristic life is typically in the range of 500 million cycles. Therefore, the bounds for the life test would be between 5 million and 350 million cycles. The maximum run cycles required is dependent upon ß, with higher run times required to verify populations with high ß. Running to 200M to 300M operations is sufficient to generate failures and provide good statistical data for most dry-reed relays.
Using Weibull for Life Predictions
The results from several life tests were examined to demonstrate the effectiveness of the Weibull distribution for these applications. Two dry-reed relays were compared in the first study. The first device was a SPST (Single Pole Single Throw) relay and the second was a FPST (Four Pole Single Throw) relay. Both life tests were set up with identical loads of 5 Volts/20 mA. A sample size of 28 devices was run to 300 million cycles for the SPST test, and 5 devices were run to 100 million cycles for the FPST test. The results are plotted on the Weibull chart in Figure 1. From this chart it can be seen that ß = 1 for both devices, which implies that these populations are in the steady state failure portion of their life cycle (failures are random and independent upon time). It can also be observed that the characteristic life () is 1400M cycles for the SPST device and 65M cycles for the FPST device. The t/ ratio is greater than one for the FPST device and is 0.21 for the SPST device. From table 1 it can be seen that the sample size of 5 for the FPST part and a sample size of 28 for the SPST part were more than sufficient to verify the reliability of these parts with good confidence.
Figure 1
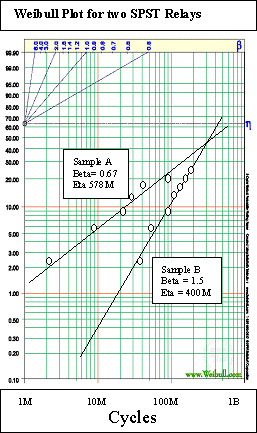
A second study was made with two SPST dry-reed relays running a 10 Volts/4 mA life test, and these results are plotted in figure 2. The sample size for both tests was 28. The life test for sample A was run to 100 million cycles and to 200 million cycles for sample B. The results for sample A show infancy with ß=0.67, while the results for sample B show some degree of wear out with ß=1.5. Eta for sample A is 578M cycles and for sample B is 400M cycles. The t/ ratio for sample A is 0.35 and for sample B is 0.5. From table 1 the minimum sample size is 5 units for sample A and 7 units for sample B. The selected sample size of 28 was more than sufficient to verify the reliability of these parts.
Figure 2
Comparing Life Tests for Electromechanical Relays versus Hard Disk Drives (HDD)
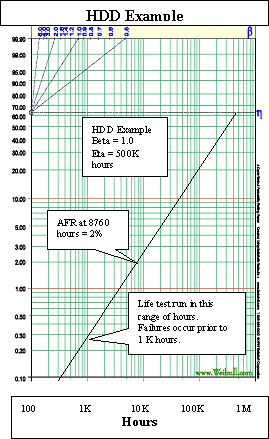
Figure 3 shows a typical Weibull plot for a HDD. From the chart it can be noted that the AFR (Annual Failure Rate) is the failure percentage at the one-year point (8760 hours of operation). Interesting comparisons can be made between the life tests for HDDs and for relays. HDDs have characteristic lives of 100K to 500K hours. Life tests for HDDs are typically run to 1,000 hours, which results in a t/ = 0.002. Assuming ß=1, the sample size required to achieve a 90% confidence level is calculated as follow:
n = (500K/1000)*ln(0.1) = 1150
Large sample sizes are required for HDDs since the ratio of test time to the characteristic life is very small. A typical HDD life test is set up with 1,000 drives running for 1,000 hours (about 6 weeks). The Weibull prediction is based upon establishing the slope (ß) with very low hours per device. Since failures occur at a time less than 1,000 hours, the Weibull plot line for HDDs is determined at the very lower left corner of the plot. This means that small changes in the failure points can have huge effects upon the predicted value for the characteristic life, . Life tests for relays can be run much closer to their total expected life, resulting in better predictions for . Also, since high cycle counts can be achieved in the life test, the ratio of test cycles to the expected life is closer to one, thus reducing the need for huge sample sizes.
Figure 3
 Conclusion
The two-parameter Weibull distribution is very well suited for use with predicting the life of electromechanical relays. The tests can be set up with relatively small sample sizes, and the results can be plotted with low numbers of failures. By accelerating the operating frequency of the relay, the total number of test cycles can be close to the characteristic life () for the part, thereby reducing the required sample size.
Weibull plots can be easily generated using commercially available software. However, assuming the data is reasonably well behaved the plots can also be done by hand. Either way it provides an excellent statistical verification of the test results. The use of the Weibull distribution is a very simple and effective tool in predicting the life for electromechanical relays.
Author:
Phil Roettjer
President, Relay Testing Services, LLC
Mendon, MA
Phil has over 20 years of experience in the development of hard disk drives. His last position prior to RTS was as the Director of Quality for the High-End Disk-Drive Division of Maxtor Corporation in Shrewsbury, Massachusetts.
Reprinted with permission from Evaluation Engineering, June 2004
Copyright © 2004 by Nelson Publishing Inc. www.evaluationengineering.com
Click here for a printable version of this article. Printable format requires Adobe Acrobat Reader which can be downloaded for free here.
|
