- Quantum entanglement.6 29 2014

https://dropithere.netlify.app/text/2YHoFbMDK1H3LDAKZCN3

http://ningspruz7.tech/button2901

No categories created.

Add Page

View All

Quantum entanglement

From Wikipedia, the free encyclopedia

Spontaneous parametric down-conversion process can split photons into type II photon pairs with mutually perpendicular polarization.

Quantum mechanics
$\Delta x\cdot\Delta p_x \geqslant \frac{\hbar}{2}$ Uncertainty principle
Introduction Glossary History
Background[show]
Fundamentals[show]
Experiments[show]
Formulations[show]
Equations[show]
Interpretations [show]
Advanced topics[show]
Scientists[show]
v t e

Quantum entanglement is a physical phenomenon that occurs when pairs or groups of particles are generated or interact in ways such that the quantum state of each particle cannot be described independently – instead, a quantum state may be given for the system as a whole.

Measurements of physical properties such as position, momentum, spin, polarization, etc. performed on entangled particles are found to be appropriately correlated. For example, if a pair of particles is generated in such a way that their total spin is known to be zero, and one particle is found to have clockwise spin on a certain axis, then the spin of the other particle, measured on the same axis, will be found to be counterclockwise. Because of the nature of quantum measurement, however, this behavior gives rise to effects that can appear paradoxical: any measurement of a property of a particle can be seen as acting on that particle (e.g. by collapsing a number of superimposed states); and in the case of entangled particles, such action must be on the entangled system as a whole. It thus appears that one particle of an entangled pair "knows" what measurement has been performed on the other, and with what outcome, even though there is no known means for such information to be communicated between the particles, which at the time of measurement may be separated by arbitrarily large distances.

Such phenomena were the subject of a 1935 paper by Albert Einstein, Boris Podolsky and Nathan Rosen,^[1] describing what came to be known as the EPR paradox, and several papers by Erwin Schrödinger shortly thereafter.^[2]^[3] Einstein and others considered such behavior to be impossible, as it violated the local realist view of causality (Einstein referred to it as "spooky action at a distance"),^[4] and argued that the accepted formulation of quantum mechanics must therefore be incomplete. Later, however, the counterintuitive predictions of quantum mechanics were verified experimentally.^[5] Experiments have been performed involving measuring the polarization or spin of entangled particles in different directions, which – by producing violations of Bell's inequality – demonstrate statistically that the local realist view cannot be correct. This has been shown to occur even when the measurements are performed more quickly than light could travel between the sites of measurement: there is no lightspeed or slower influence that can pass between the entangled particles.^[6] Recent experiments have measured entangled particles within less than one part in 10,000 of the light travel time between them.^[7] According to the formalism of quantum theory, the effect of measurement happens instantly.^[8]^[9] It is not possible, however, to use this effect to transmit classical information at faster-than-light speeds^[10] (see Faster-than-light → Quantum mechanics).

Quantum entanglement is an area of extremely active research by the physics community, and its effects have been demonstrated experimentally with photons, electrons, molecules the size of buckyballs,^[11]^[12] and even small diamonds.^[13]^[14] Research is also focused on the utilization of entanglement effects in communication and computation.

History

May 4, 1935 New York Times article headline regarding the imminent EPR paper.

The counterintuitive predictions of quantum mechanics about strongly correlated systems were first discussed by Albert Einstein in 1935, in a joint paper with Boris Podolsky and Nathan Rosen.^[1] In this study, they formulated the EPR paradox (Einstein, Podolsky, Rosen paradox), a thought experiment that attempted to show that quantum mechanical theory was incomplete. They wrote: "We are thus forced to conclude that the quantum-mechanical description of physical reality given by wave functions is not complete."^[1]

However, they did not coin the word entanglement, nor did they generalize the special properties of the state they considered. Following the EPR paper, Erwin Schrödinger wrote a letter (in German) to Einstein in which he used the word Verschränkung (translated by himself as entanglement) "to describe the correlations between two particles that interact and then separate, as in the EPR experiment."^[15] He shortly thereafter published a seminal paper defining and discussing the notion, and terming it "entanglement." In the paper he recognized the importance of the concept, and stated:^[2] "I would not call [entanglement] one but rather the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought."

Like Einstein, Schrödinger was dissatisfied with the concept of entanglement, because it seemed to violate the speed limit on the transmission of information implicit in the theory of relativity.^[16] Einstein later famously derided entanglement as "spukhafte Fernwirkung"^[17] or "spooky action at a distance."

The EPR paper generated significant interest among physicists and inspired much discussion about the foundations of quantum mechanics (perhaps most famously Bohm's interpretation of quantum mechanics), but relatively little other published work. So, despite the interest, the flaw in EPR's argument was not discovered until 1964, when John Stewart Bell proved that one of their key assumptions, the principle of locality, was not consistent with the hidden variables interpretation of quantum theory that EPR purported to establish. Specifically, he demonstrated an upper limit, seen in Bell's inequality, regarding the strength of correlations that can be produced in any theory obeying local realism, and he showed that quantum theory predicts violations of this limit for certain entangled systems.^[18] His inequality is experimentally testable, and there have been numerous relevant experiments, starting with the pioneering work of Freedman and Clauser in 1972^[19] and Aspect's experiments in 1982.^[20] They have all shown agreement with quantum mechanics rather than the principle of local realism. However, the issue is not finally settled, for each of these experimental tests has left open at least one loophole by which it is possible to question the validity of the results.

The work of Bell raised the possibility of using these super strong correlations as a resource for communication. It led to the discovery of quantum key distribution protocols, most famously BB84 by Bennet and Brassard and E91 by Artur Ekert. Although BB84 does not use entanglement, Ekert's protocol uses the violation of a Bell's inequality as a proof of security.

David Kaiser of MIT mentioned in his book, How the Hippies Saved Physics, that the possibilities of instantaneous long-range communication derived from Bell's theorem stirred interest among hippies, psychics, and even the CIA, with the counter-culture playing a critical role in its development toward practical use.^[21]

Concept

Meaning of entanglement

Quantum systems can become entangled through various types of interactions. (For some ways in which entanglement may be achieved for experimental purposes, see the section below on methods.) An entangled system has a quantum state which cannot be factored out into the product of states of its local constituents (e.g. individual particles). If entangled, one constituent cannot be fully described without considering the other(s). Like the quantum states of individual particles, the state of an entangled system is expressible as a sum, or superposition, of basis states, which are eigenstates of some observable(s). Entanglement is broken when the entangled particles decohere through interaction with the environment; for example, when a measurement is made.^[22]

An example of entanglement occurs when a subatomic particle decays into a pair of other particles. These decay events obey the various conservation laws, and as a result, the measurement outcomes of one daughter particle must be highly correlated with the measurement outcomes of the other daughter particle (so that the total momenta, angular momenta, energy, and so forth remains roughly the same before and after this process). For instance, a spin-zero particle could decay into a pair of spin-1/2 particles. Since the total spin before and after this decay must be zero (conservation of angular momentum), whenever the first particle is measured to be spin up on some axis, the other (when measured on the same axis) is always found to be spin down. (This is called the spin anti-correlated case; and if the prior probabilities for measuring each spin are equal, the pair is said to be in the singlet state.)

Apparent paradox

The seeming paradox here is that a measurement made on either of the particles apparently collapses the state of the entire entangled system – and does so instantaneously, before any information about the measurement could have reached the other particle (assuming that information cannot travel faster than light). In the quantum formalism, the result of a spin measurement on one of the particles is a collapse into a state in which each particle has a definite spin (either up or down) along the axis of measurement. The outcome is taken to be random, with each possibility having a probability of 50%. However, if both spins are measured along the same axis, they are found to be anti-correlated. This means that the random outcome of the measurement made on one particle seems to have been transmitted to the other, so that it can make the "right choice" when it is measured. The distance and timing of the measurements can be chosen so as to make the interval between the two measurements spacelike, i.e. from any of the two measuring events to the other a message would have to travel faster than light. Then, according to the principles of special relativity, it is not in fact possible for any information to travel between two such measuring events – it is not even possible to say which of the measurements came first, as this would depend on the inertial system of the observer. Therefore the correlation between the two measurements cannot appropriately be explained as one measurement determining the other: different observers would disagree about the role of cause and effect.

The hidden variables theory

A possible resolution to the apparent paradox might be to assume that the state of the particles contains some hidden variables, whose values effectively determine, right from the moment of separation, what the outcomes of the spin measurements are going to be. This would mean that each particle carries all the required information with it, and nothing needs to be transmitted from one particle to the other at the time of measurement. It was originally believed by Einstein and others (see the previous section) that this was the only way out, and therefore that the accepted quantum mechanical description (with a random measurement outcome) must be incomplete. (In fact similar paradoxes can arise even without entanglement: the position of a single particle is spread out over space, and two detectors attempting to detect the particle at different positions must attain appropriate correlation, so that they do not both detect the particle.)

Violations of Bell's inequality

The hidden variables theory fails, however, when we consider measurements of the spin of entangled particles along different axes (for example, along any of three axes which make angles of 120 degrees). If a large number of pairs of such measurements are made (on a large number of pairs of entangled particles), then statistically, if the local realist or hidden variables view were correct, the results would always satisfy Bell's inequality. A number of experiments have shown in practice, however, that Bell's inequality is not satisfied. This tends to confirm that the original formulation of quantum mechanics is indeed correct, in spite of its apparently paradoxical nature. Even when measurements of the entangled particles are made in moving relativistic reference frames, in which each measurement (in its own relativistic time frame) occurs before the other, the measurement results remain correlated.^[23]^[24]

The fundamental issue about measuring spin along different axes is that these measurements cannot have definite values at the same time―they are incompatible in the sense that these measurements' maximum simultaneous precision is constrained by the uncertainty principle. This is contrary to what is found in classical physics, where any number of properties can be measured simultaneously with arbitrary accuracy. It has been proven mathematically that compatible measurements cannot show Bell-inequality-violating correlations,^[25] and thus entanglement is a fundamentally non-classical phenomenon.

Other types of experiment

In a 2012 experiment, "delayed-choice entanglement swapping" was used to decide whether two particles were entangled or not after they had already been measured.^[26]

In a 2013 experiment, entanglement swapping has been used to create entanglement between photons that never coexisted in time, thus demonstrating that "the nonlocality of quantum mechanics, as manifested by entanglement, does not apply only to particles with spacelike separation, but also to particles with timelike [i.e., temporal] separation".^[27]

In three independent experiments it was shown that classically-communicated separable quantum states can be used carry entangled states.^[28]

Special Theory of Relativity

Another theory explains quantum entanglement using special relativity.^[29] According to this theory, faster-than-light communication between entangled systems can be achieved because the time dilation of special relativity allows time to stand still in light's point of view. For example, in the case of two entangled photons, a measurement made on one photon at present time would determine the state of the photon for both the present and past at the same moment. This leads to the instantaneous determination of the state of the other photon. Corresponding logic is applied to explain entangled systems, i.e. electron and positron, that travel below the speed of light.

Non-locality and hidden variables

There is much confusion about the meaning of entanglement, non-locality and hidden variables and how they relate to each other. As described above, entanglement is an experimentally verified and accepted property of nature, which has critical implications for the interpretations of quantum mechanics. The question becomes, "How can one account for something that was at one point indefinite with regard to its spin (or whatever is in this case the subject of investigation) suddenly becoming definite in that regard even though no physical interaction with the second object occurred, and, if the two objects are sufficiently far separated, could not even have had the time needed for such an interaction to proceed from the first to the second object?"^[30] The latter question involves the issue of locality, i.e., whether for a change to occur in something the agent of change has to be in physical contact (at least via some intermediary such as a field force) with the thing that changes. Study of entanglement brings into sharp focus the dilemma between locality and the completeness or lack of completeness of quantum mechanics.

Bell's theorem and related results rule out a local realistic explanation for quantum mechanics (one which obeys the principle of locality while also ascribing definite values to quantum observables). However, in other interpretations, the experiments that demonstrate the apparent non-locality can also be described in local terms: If each distant observer regards the other as a quantum system, communication between the two must then be treated as a measurement process, and this communication is strictly local.^[31] In particular, in the many worlds interpretation, the underlying description is fully local.^[32] More generally, the question of locality in quantum physics is extraordinarily subtle and sometimes hinges on precisely how it is defined.

In the media and popular science, quantum non-locality is often portrayed as being equivalent to entanglement. While it is true that a bipartite quantum state must be entangled in order for it to produce non-local correlations, there exist entangled states that do not produce such correlations. A well-known example of this is the Werner state that is entangled for certain values of 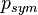$p_{sym}$ , but can always be described using local hidden variables.^[33] In short, entanglement of a two-party state is necessary but not sufficient for that state to be non-local. It is important to recognise that entanglement is more commonly viewed as an algebraic concept, noted for being a precedent to non-locality as well as to quantum teleportation and to superdense coding, whereas non-locality is defined according to experimental statistics and is much more involved with the foundations and interpretations of quantum mechanics.

Quantum mechanical framework

The following subsections are for those with a good working knowledge of the formal, mathematical description of quantum mechanics, including familiarity with the formalism and theoretical framework developed in the articles: bra–ket notation and mathematical formulation of quantum mechanics.

Pure states

Consider two noninteracting systems $A$ and $B$ , with respective Hilbert spaces $H A$ and $H B$ . The Hilbert space of the composite system is the tensor product

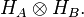
H_A \otimes H_B.

If the first system is in state 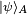$\scriptstyle| \psi \rangle_A$ and the second in state $\scriptstyle| \phi \rangle_B$ , the state of the composite system is

|\psi\rangle_A \otimes |\phi\rangle_B.

States of the composite system which can be represented in this form are called separable states, or (in the simplest case) product states.

Not all states are separable states (and thus product states). Fix a basis $\scriptstyle \{|i \rangle_A\}$ for $H A$ and a basis $\scriptstyle \{|j \rangle_B\}$ for $H B$ . The most general state in $H A \otimes H B$ is of the form

|\psi\rangle_{AB} = \sum_{i,j} c_{ij} |i\rangle_A \otimes |j\rangle_B

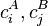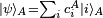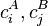This state is separable if there exist $c^A_i,c^B_j$ so that $\scriptstyle c_{ij}= c^A_ic^B_j,$ yielding $\scriptstyle |\psi\rangle_A = \sum_{i} c^A_{i} |i\rangle_A$ and $\scriptstyle |\phi\rangle_B = \sum_{j} c^B_{j} |j\rangle_B.$ It is inseparable if for all $c^A_i,c^B_j$ we have $\scriptstyle c_{ij} \neq c^A_ic^B_j.$ If a state is inseparable, it is called an entangled state.

For example, given two basis vectors $\scriptstyle \{|0\rangle_A, |1\rangle_A\}$ of $H A$ and two basis vectors $\scriptstyle \{|0\rangle_B, |1\rangle_B\}$ of $H B$ , the following is an entangled state:

\tfrac{1}{\sqrt{2}} \left ( |0\rangle_A \otimes |1\rangle_B - |1\rangle_A \otimes |0\rangle_B \right ).

If the composite system is in this state, it is impossible to attribute to either system $A$ or system $B$ a definite pure state. Another way to say this is that while the von Neumann entropy of the whole state is zero (as it is for any pure state), the entropy of the subsystems is greater than zero. In this sense, the systems are "entangled". This has specific empirical ramifications for interferometry.^[34] It is worthwhile to note that the above example is one of four Bell states, which are (maximally) entangled pure states (pure states of the $H A \otimes H B$ space, but which cannot be separated into pure states of each $H A$ and $H B$ ).

Now suppose Alice is an observer for system $A$ , and Bob is an observer for system $B$ . If in the entangled state given above Alice makes a measurement in the $\scriptstyle \{|0\rangle, |1\rangle\}$ eigenbasis of $A$ , there are two possible outcomes, occurring with equal probability:^[35]

Alice measures 0, and the state of the system collapses to $\scriptstyle |0\rangle_A |1\rangle_B$ .
Alice measures 1, and the state of the system collapses to $\scriptstyle |1\rangle_A |0\rangle_B$ .

If the former occurs, then any subsequent measurement performed by Bob, in the same basis, will always return 1. If the latter occurs, (Alice measures 1) then Bob's measurement will return 0 with certainty. Thus, system $B$ has been altered by Alice performing a local measurement on system $A$ . This remains true even if the systems $A$ and $B$ are spatially separated. This is the foundation of the EPR paradox.

The outcome of Alice's measurement is random. Alice cannot decide which state to collapse the composite system into, and therefore cannot transmit information to Bob by acting on her system. Causality is thus preserved, in this particular scheme. For the general argument, see no-communication theorem.

Ensembles

As mentioned above, a state of a quantum system is given by a unit vector in a Hilbert space. More generally, if one has a large number of copies of the same system, then the state of this ensemble is described by a density matrix, which is a positive-semidefinite matrix, or a trace class when the state space is infinite-dimensional, and has trace 1. Again, by the spectral theorem, such a matrix takes the general form:

\rho = \sum_i w_i |\alpha_i\rangle \langle\alpha_i|,

where the positive valued $w i$ sum up to 1, and in the infinite-dimensional case, we would take the closure of such states in the trace norm. We can interpret $ρ$ as representing an ensemble where $w i$ is the proportion of the ensemble whose states are $|\alpha_i\rangle$ . When a mixed state has rank 1, it therefore describes a pure ensemble. When there is less than total information about the state of a quantum system we need density matrices to represent the state.

Following the definition in previous section, for a bipartite composite system, mixed states are just density matrices on $H A \otimes H B$ . Extending the definition of separability from the pure case, we say that a mixed state is separable if it can be written as^[36]^:131–132

\rho = \sum_i p_i \rho_i^A \otimes \rho_i^B,

where $p i$ are positive valued probabilities, $\rho_i^A$ 's and $\rho_i^B$ 's are themselves states on the subsystems $A$ and $B$ respectively. In other words, a state is separable if it is a probability distribution over uncorrelated states, or product states. We can assume without loss of generality that $\rho_i^A$ and $\rho_i^B$ are pure ensembles. A state is then said to be entangled if it is not separable. In general, finding out whether or not a mixed state is entangled is considered difficult. The general bipartite case has been shown to be NP-hard.^[37] For the $2 \times 2$ and $2 \times 3$ cases, a necessary and sufficient criterion for separability is given by the famous Positive Partial Transpose (PPT) condition.^[38]

Experimentally, a mixed ensemble might be realized as follows. Consider a "black-box" apparatus that spits electrons towards an observer. The electrons' Hilbert spaces are identical. The apparatus might produce electrons that are all in the same state; in this case, the electrons received by the observer are then a pure ensemble. However, the apparatus could produce electrons in different states. For example, it could produce two populations of electrons: one with state $|\mathbf{z}+\rangle$ with spins aligned in the positive $z$ direction, and the other with state $|\mathbf{y}-\rangle$ with spins aligned in the negative $y$ direction. Generally, this is a mixed ensemble, as there can be any number of populations, each corresponding to a different state.

Reduced density matrices

The idea of a reduced density matrix was introduced by Paul Dirac in 1930.^[39] Consider as above systems $A$ and $B$ each with a Hilbert space $H A, H B$ . Let the state of the composite system be

|\Psi \rangle \in H_A \otimes H_B.

As indicated above, in general there is no way to associate a pure state to the component system $A$ . However, it still is possible to associate a density matrix. Let

\rho_T = |\Psi\rangle \; \langle\Psi|

which is the projection operator onto this state. The state of $A$ is the partial trace of $ρ T$ over the basis of system $B$ :

\rho_A \ \stackrel{\mathrm{def}}{=}\ \sum_j \langle j|_B \left( |\Psi\rangle \langle\Psi| \right) |j\rangle_B = \hbox{Tr}_B \; \rho_T.

$ρ A$ is sometimes called the reduced density matrix of $ρ$ on subsystem $A$ . Colloquially, we "trace out" system $B$ to obtain the reduced density matrix on $A$ .

For example, the reduced density matrix of $A$ for the entangled state

\tfrac{1}{\sqrt{2}} \left ( |0\rangle_A \otimes |1\rangle_B - |1\rangle_A \otimes |0\rangle_B \right),

discussed above is

\rho_A = \tfrac{1}{2} \left ( |0\rangle_A \langle 0|_A + |1\rangle_A \langle 1|_A \right )

This demonstrates that, as expected, the reduced density matrix for an entangled pure ensemble is a mixed ensemble. Also not surprisingly, the density matrix of $A$ for the pure product state $|\psi\rangle_A \otimes |\phi\rangle_B$ discussed above is

\rho_A = |\psi\rangle_A \langle\psi|_A .

In general, a bipartite pure state ρ is entangled if and only if its reduced states are mixed rather than pure. Reduced density matrices were explicitly calculated in different spin chains with unique ground state. An example is the one-dimensional AKLT spin chain:^[40] the ground state can be divided into a block and an environment. The reduced density matrix of the block is proportional to a projector to a degenerate ground state of another Hamiltonian.

The reduced density matrix also was evaluated for XY spin chains, where it has full rank. It was proved that in the thermodynamic limit, the spectrum of the reduced density matrix of a large block of spins is an exact geometric sequence^[41] in this case.

Entropy

In this section, the entropy of a mixed state is discussed as well as how it can be viewed as a measure of quantum entanglement.

Definition

The plot of von Neumann entropy Vs Eigenvalue for a bipartite 2-level pure state. When the eigenvalue has value .5, von Neumann entropy is at a maximum, corresponding to maximum entanglement.

In classical information theory, the Shannon entropy, $H$ is associated to a probability distribution, $p_1, \cdots, p_n$ , in the following way:^[42]

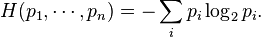
H(p_1, \cdots, p_n ) = - \sum_i p_i \log_2 p_i.

Since a mixed state $ρ$ is a probability distribution over an ensemble, this leads naturally to the definition of the von Neumann entropy:

S(\rho) = - \hbox{Tr} \left( \rho \log_2 {\rho} \right).

In general, one uses the Borel functional calculus to calculate $log(ρ)$ . If $ρ$ acts on a finite-dimensional Hilbert space and has eigenvalues $\lambda_1, \cdots, \lambda_n$ , the Shannon entropy is recovered:

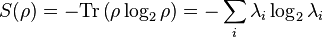S(\rho) = - \hbox{Tr} \left( \rho \log_2 {\rho} \right) = - \sum_i \lambda_i \log_2 \lambda_i

Since an event of probability 0 should not contribute to the entropy, and given that

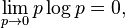
\lim_{p \to 0} p \log p = 0,

the convention $0 log(0) = 0$ is adopted. This extends to the infinite-dimensional case as well: if $ρ$ has spectral resolution

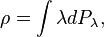
\rho = \int \lambda d P_{\lambda},

assume the same convention when calculating

\rho \log_2 \rho = \int \lambda \log_2 \lambda d P_{\lambda}.

As in statistical mechanics, the more uncertainty (number of microstates) the system should possess, the larger the entropy. For example, the entropy of any pure state is zero, which is unsurprising since there is no uncertainty about a system in a pure state. The entropy of any of the two subsystems of the entangled state discussed above is $log(2)$ (which can be shown to be the maximum entropy for $2 \times 2$ mixed states).

As a measure of entanglement

Entropy provides one tool which can be used to quantify entanglement, although other entanglement measures exist.^[43] If the overall system is pure, the entropy of one subsystem can be used to measure its degree of entanglement with the other subsystems.

For bipartite pure states, the von Neumann entropy of reduced states is the unique measure of entanglement in the sense that it is the only function on the family of states that satisfies certain axioms required of an entanglement measure.

It is a classical result that the Shannon entropy achieves its maximum at, and only at, the uniform probability distribution {1/n,...,1/n}. Therefore, a bipartite pure state $ρ \in H \otimes H$ is said to be a maximally entangled state if the reduced state of $ρ$ is the diagonal matrix

\begin{bmatrix} \frac{1}{n}& & \\ & \ddots & \\ & & \frac{1}{n}\end{bmatrix}.

For mixed states, the reduced von Neumann entropy is not the unique entanglement measure.

As an aside, the information-theoretic definition is closely related to entropy in the sense of statistical mechanics^{[citation needed]} (comparing the two definitions, we note that, in the present context, it is customary to set the Boltzmann constant $k = 1$ ). For example, by properties of the Borel functional calculus, we see that for any unitary operator $U$ ,

S(\rho) = S \left (U \rho U^* \right).

Indeed, without the above property, the von Neumann entropy would not be well-defined. In particular, $U$ could be the time evolution operator of the system, i.e.

U(t) = \exp \left(\frac{-i H t }{\hbar}\right),

where $H$ is the Hamiltonian of the system. This associates the reversibility of a process with its resulting entropy change, i.e., a process is reversible if, and only if, it leaves the entropy of the system invariant. This provides a connection between quantum information theory and thermodynamics. Rényi entropy also can be used as a measure of entanglement.

Therefore the march of the arrow of time towards thermodynamic equilibrium is simply the growing spread of quantum entanglement.^[44]

Quantum field theory

The Reeh-Schlieder theorem of quantum field theory is sometimes seen as an analogue of quantum entanglement.

Applications

Entanglement has many applications in quantum information theory. With the aid of entanglement, otherwise impossible tasks may be achieved.

Among the best-known applications of entanglement are superdense coding and quantum teleportation.^[45]

Most researchers believe that entanglement is necessary to realize quantum computing (although this is disputed by some^[46]).

Entanglement is used in some protocols of quantum cryptography.^[47]^[48] This is because the "shared noise" of entanglement makes for an excellent one-time pad. Moreover, since measurement of either member of an entangled pair destroys the entanglement they share, entanglement-based quantum cryptography allows the sender and receiver to more easily detect the presence of an interceptor.

In interferometry, entanglement is necessary for surpassing the standard quantum limit and achieving the Heisenberg limit.

Entangled states

There are several canonical entangled states that appear often in theory and experiments.

For two qubits, the Bell states are

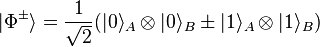
|\Phi^\pm\rangle = \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |0\rangle_B \pm |1\rangle_A \otimes |1\rangle_B)

|\Psi^\pm\rangle = \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |1\rangle_B \pm |1\rangle_A \otimes |0\rangle_B)

These four pure states are all maximally entangled (according to the entropy of entanglement) and form an orthonormal basis (linear algebra) of the Hilbert space of the two qubits. They play a fundamental role in Bell's theorem.

For M>2 qubits, the GHZ state is

|\mathrm{GHZ}\rangle = \frac{|0\rangle^{\otimes M} + |1\rangle^{\otimes M}}{\sqrt{2}},

which reduces to the Bell state 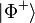$|\Phi^+\rangle$ for $M=2$ . The traditional GHZ state was defined for $M=3$ . GHZ states are occasionally extended to qudits, i.e. systems of d rather than 2 dimensions.

Also for M>2 qubits, there are spin squeezed states.^[49] Spin squeezed states are a class of states satisfying certain restrictions on the uncertainty of spin measurements, and are necessarily entangled.^[50]

For two bosonic modes, a NOON state is

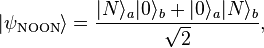
|\psi_\text{NOON} \rangle = \frac{|N \rangle_a |0\rangle_b + |{0}\rangle_a |{N}\rangle_b}{\sqrt{2}}, \,

This is like a Bell state 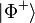$|\Phi^+\rangle$ except the basis kets 0 and 1 have been replaced with "the N photons are in one mode" and "the N photons are in the other mode".

Finally, there also exist twin Fock states for bosonic modes, which can be created by feeding a Fock state into two arms leading to a beam-splitter. They are the sum of multiple of NOON states, and can used to achieve the Heisenberg limit.^[51]

For the appropriately chosen measure of entanglement, Bell, GHZ, and NOON states are maximally entangled while spin squeezed and twin Fock states are only partially entangled. The partially entangled states are generally easier to prepare experimentally.

Methods of creating entanglement

Entanglement is usually created by direct interactions between subatomic particles. These interactions can take numerous forms. One of the most commonly used methods is spontaneous parametric down-conversion to generate a pair of photons entangled in polarisation.^[52] Other methods include the use of a fiber coupler to confine and mix photons, the use of quantum dots to trap electrons until decay occurs, the use of the Hong-Ou-Mandel effect, etc. In the earliest tests of Bell's theorem, the entangled particles were generated using atomic cascades.

It is also possible to create entanglement between quantum systems that never directly interacted, through the use of entanglement swapping.

Author:	Bling King
Published:	Jun 29th 2014
Modified:	Jun 29th 2014

Quantum entanglement

Quantum entanglement

Contents

History

Concept

Meaning of entanglement

Apparent paradox

The hidden variables theory

Violations of Bell's inequality

Other types of experiment

Special Theory of Relativity

Non-locality and hidden variables

Quantum mechanical framework

Pure states

Ensembles

Reduced density matrices

Entropy

Definition

As a measure of entanglement

Quantum field theory

Applications

Entangled states

Methods of creating entanglement