- Fixed rate mortgage.5 19 2012

https://dropithere.netlify.app/text/2YHoFbMDK1H3LDAKZCN3

http://ningspruz7.tech/button2901

No categories created.

Add Page

View All

Fixed-rate mortgage

A fixed-rate mortgage (FRM), often referred to as a "plain vanilla" mortgage loan, is a fully amortizing mortgage loan where the interest rate on the note remains the same through the term of the loan, as opposed to loans where the interest rate may adjust or "float". As a result, payment amounts and the duration of the loan are fixed.

Other forms of mortgage loans include interest only mortgage, graduated payment mortgage, variable rate (including adjustable rate mortgages and tracker mortgages), negative amortization mortgage, and balloon payment mortgage. Unlike many other loan types, FRM interest payments and loan duration is fixed from beginning to end.

Fixed-rate mortgages are characterized by amount of loan, interest rate, compounding frequency, and duration. With these values, the monthly repayments can be calculated.

Overview

Unlike adjustable rate mortgages (ARM), fixed-rate mortgages are not tied to an index. Instead, the interest rate is set (or "fixed") in advance to an advertised rate, usually in increments of 1/4 or 1/8 percent.

The fixed monthly payment for a fixed-rate mortgage is the amount paid by the borrower every month that ensures that the loan is paid off in full with interest at the end of its term.

Popularity

The United States Federal Housing Administration (FHA) helped develop and standardize the fixed rate mortgage as an alternative to the balloon payment mortgage by insuring them and by doing so helped the mortgage design garner usage.^[1] Because of the large payment at the end of the loan, refinancing risk resulted in widespread foreclosures. It was the first mortgage loan that was fully amortized (fully paid at the end of the loan) precluding successive loans, and had fixed interest rates and payments.

Fixed-rate mortgages are the most classic form of loan for home and product purchasing in the United States. The most common terms are 15-year and 30-year mortgages, but shorter terms are available, and 40-year and 50-year mortgages are now available (common in areas with high priced housing, where even a 30-year term leaves the mortgage amount out of reach of the average family).

Outside the United States, fixed-rate mortgages are less popular, and in some countries, true fixed-rate mortgages are not available except for shorter-term loans. For example, in Canada the longest term for which a mortgage rate can be fixed is typically no more than ten years, while mortgage maturities are commonly 25 years.

Comparisons

Fixed rate mortgages are usually more expensive than adjustable rate mortgages. Due to the inherent interest rate risk, long-term fixed rate loans will tend to be at a higher interest rate than short-term loans. The relationship between interest rates for short and long-term loans is represented by the yield curve, which generally slopes upward (longer terms are more expensive). The opposite circumstance is known as an inverted yield curve and occurs less often.

The fact that a fixed rate mortgage has a higher starting interest rate does not indicate that this is a worse form of borrowing compared to the adjustable rate mortgages. If interest rates rise, the ARM cost will be higher while the FRM will remain the same. In effect, the lender has agreed to take the interest rate risk on a fixed-rate loan. Some studies ^[2] have shown that the majority of borrowers with adjustable rate mortgages save money in the long term, but that some borrowers pay more. The price of potentially saving money, in other words, is balanced by the risk of potentially higher costs. In each case, a choice would need to be made based upon the loan term, the current interest rate, and the likelihood that the rate will increase or decrease during the life of the loan.

Pricing

Note: Fixed-rate mortgage interest may be compounded differently in other countries, such as in Canada, where it is compounded every 6 months.

The fixed monthly payment for a fixed rate mortgage is the amount paid by the borrower every month that ensures that the loan is paid off in full with interest at the end of its term. This monthly payment $c$ depends upon the monthly interest rate $r$ (expressed as a fraction, not a percentage, i.e., divide the quoted yearly nominal percentage rate by 100 and by 12 to obtain the monthly interest rate), the number of monthly payments $N$ called the loan's term, and the amount borrowed $P_0$ known as the loan's principal; rearranging the formula for the present value of an ordinary annuity we get the formula for $c$ :

$c = {r\over{1-(1+r)^{-N}}}P_0$

For example, for a home loan for $200,000 with a fixed yearly nominal interest rate of 6.5% for 30 years, the principal is $P_0=200000$ , the monthly interest rate is $r=6.5/100/12$ , the number of monthly payments is $N=30*12=360$ , the fixed monthly payment $c=$1264.14$ . This formula is provided using the financial function PMT in a spreadsheet such as Excel. In the example, the monthly payment is obtained by entering either of the these formulas:

=PMT(6.5/100/12,30*12,200000)

=((6.5/100/12)/(1-(1+6.5/100/12)^(-30*12)))*200000

${}=1264.14$

This monthly payment formula is easy to derive, and the derivation illustrates how fixed-rate mortgage loans work. The amount owed on the loan at the end of every month equals the amount owed from the previous month, plus the interest on this amount, minus the fixed amount paid every month.

Amount owed at month 0:

$P_0$

Amount owed at month 1:

$P_1 = P_0+P_0*r-c$ ( principal + interest – payment)

$P_1 = P_0(1+r)-c$ (equation 1)

Amount owed at month 2:

$P_2 = P_1(1+r)-c$

Using equation 1 for $P_1$

$P_2 = (P_0(1+r)-c)(1+r)-c$

$P_2 = P_0(1+r)^2- c(1+r)- c$ (equation 2)

Amount owed at month 3:

$P_3 = P_2(1+r) - c$

Using equation 2 for $P_2$

$P_3 = (P_0(1+r)^2- c(1+r)- c)(1+r) - c$

$P_3 = P_0(1+r)^3- c(1+r)^2- c(1+r) - c$

Amount owed at month N:

$P_N = P_{N-1}(1+r) - c$

$P_N = P_0(1+r)^N - c(1+r)^{N-1} - c(1+r)^{N-2} .... - c$

$P_N = P_0(1+r)^N - c ((1+r)^{N-1} + (1+r)^{N-2} .... + 1)$

$P_N = P_0(1+r)^N - c (S)$ (equation 3)

Where $S = (1+r)^{N-1} + (1+r)^{N-2} .... + 1$ (equation 4) (see geometric progression)

$S(1+r) = (1+r)^N + (1+r)^{N-1} .... + (1+r)$ (equation 5)

With the exception of two terms the 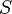$S$ and $S(1+r)$ series are the same so when you subtract all but two terms cancel:

Using equation 4 and 5

$S(1+r)-S = (1+r)^N - 1$

$S((1+r)-1) = (1+r)^N - 1$

$S(r) = (1+r)^N - 1$

$S = {{(1+r)^N - 1}\over r}$ (equation 6)

Putting equation 6 back into 3:

$P_N = P_0(1+r)^N - c {{(1+r)^N - 1}\over r}$

$P_N$ will be zero because we have paid the loan off.

$0 = P_0(1+r)^N - c {{(1+r)^N - 1}\over r}$

We want to know $c$

$c = {{r(1+r)^N} \over {(1+r)^N-1}} P_0$

Divide top and bottom with $(1+r)^N$

$c = {r \over {1-(1+r)^{-N}}} P_0$

This derivation illustrates three key components of fixed-rate loans: (1) the fixed monthly payment depends upon the amount borrowed, the interest rate, and the length of time over which the loan is repaid; (2) the amount owed every month equals the amount owed from the previous month plus interest on that amount, minus the fixed monthly payment; (3) the fixed monthly payment is chosen so that the loan is paid off in full with interest at the end of its term and no more money is owed.

Author:	Bling King
Published:	May 19th 2012
Modified:	May 19th 2012

Fixed-rate mortgage

Contents

Overview

Popularity

Comparisons

Pricing